3604: [CSP-S 2022] 星战galaxy.cpp
内存限制:512 MB
时间限制:2.000 S
评测方式:文本比较
命题人:
提交:1
解决:0
题目描述
题目描述
在这一轮的星际战争中,我方在宇宙中建立了 nnn 个据点,以 mmm 个单向虫洞连接。我们把终点为据点 uuu 的所有虫洞归为据点 uuu 的虫洞。
战火纷飞之中这些虫洞很难长久存在,敌人的打击随时可能到来。这些打击中的有效打击可以分为两类:
为了抗击敌人并维护各部队和各据点之间的联系,我方发展出了两种特种部队负责修复虫洞:
我方掌握了一种苛刻的空间特性,利用这一特性我方战舰可以沿着虫洞瞬移到敌方阵营,实现精确打击。
为了把握发动反攻的最佳时机,指挥部必须关注战场上的所有变化,为了寻找一个能够进行反攻的时刻。总指挥认为:
战火纷飞之中这些虫洞很难长久存在,敌人的打击随时可能到来。这些打击中的有效打击可以分为两类:
-
敌人会摧毁某个虫洞,这会使它连接的两个据点无法再通过这个虫洞直接到达,但这样的打击无法摧毁它连接的两个据点。
-
敌人会摧毁某个据点,由于虫洞的主要技术集中在出口处,这会导致该据点的所有还未被摧毁的虫洞被一同摧毁。而从这个据点出发的虫洞则不会摧毁。
为了抗击敌人并维护各部队和各据点之间的联系,我方发展出了两种特种部队负责修复虫洞:
-
A 型特种部队则可以将某个特定的虫洞修复。
-
B 型特种部队可以将某据点的所有损坏的虫洞修复。
我方掌握了一种苛刻的空间特性,利用这一特性我方战舰可以沿着虫洞瞬移到敌方阵营,实现精确打击。
为了把握发动反攻的最佳时机,指挥部必须关注战场上的所有变化,为了寻找一个能够进行反攻的时刻。总指挥认为:
-
如果从我方的任何据点出发,在选择了合适的路线的前提下,可以进行无限次的虫洞穿梭(可以多次经过同一据点或同一虫洞),那么这个据点就可以实现反击。
-
为了使虫洞穿梭的过程连续,尽量减少战舰在据点切换虫洞时的质能损耗,当且仅当只有一个从该据点出发的虫洞可用时,这个据点可以实现连续穿梭。
-
如果我方所有据点都可以实现反击,也都可以实现连续穿梭,那么这个时刻就是一个绝佳的反攻时刻。
输入
输入描述
从文件 galaxy.in 中读入数据。
输入的第一行包含两个正整数 n,mn,mn,m。
接下来 mmm 行每行两个数 u,vu,vu,v,表示一个从据点 uuu 出发到据点 vvv 的虫洞。保证 u≠vu \ne vu=v,保证不会有两条相同的虫洞。初始时所有的虫洞和据点都是完好的。
接下来一行一个正整数 qqq 表示询问个数。
接下来 qqq 行每行表示一次询问或操作。首先读入一个正整数 ttt 表示指令类型:
输入的第一行包含两个正整数 n,mn,mn,m。
接下来 mmm 行每行两个数 u,vu,vu,v,表示一个从据点 uuu 出发到据点 vvv 的虫洞。保证 u≠vu \ne vu=v,保证不会有两条相同的虫洞。初始时所有的虫洞和据点都是完好的。
接下来一行一个正整数 qqq 表示询问个数。
接下来 qqq 行每行表示一次询问或操作。首先读入一个正整数 ttt 表示指令类型:
-
若 t=1t = 1t=1,接下来两个整数 u,vu, vu,v 表示敌人摧毁了从据点 uuu 出发到据点 vvv 的虫洞。保证该虫洞存在且未被摧毁。
-
若 t=2t = 2t=2,接下来一个整数 uuu 表示敌人摧毁了据点 uuu。如果该据点的虫洞已全部 被摧毁,那么这次袭击不会有任何效果。
-
若 t=3t = 3t=3,接下来两个整数 u,vu, vu,v 表示我方修复了从据点 uuu 出发到据点 vvv 的虫洞。保证该虫洞存在且被摧毁。
-
若 t=4t = 4t=4,接下来一个整数 uuu 表示我方修复了据点 uuu。如果该据点没有被摧毁的虫洞,那么这次修复不会有任何效果。
输出
输出到文件 galaxy.out 中。
输出一共 qq 行。对于每个指令,输出这个指令执行后能否进行反攻。
样例输入 复制
3 6
2 3
2 1
1 2
1 3
3 1
3 2
11
1 3 2
1 2 3
1 1 3
1 1 2
3 1 3
3 3 2
2 3
1 3 1
3 1 3
4 2
1 3 2样例输出 复制
NO
NO
YES
NO
YES
NO
NO
NO
YES
NO
NO提示
【样例解释 #1】
虫洞状态可以参考下面的图片, 图中的边表示存在且未被摧毁的虫洞:
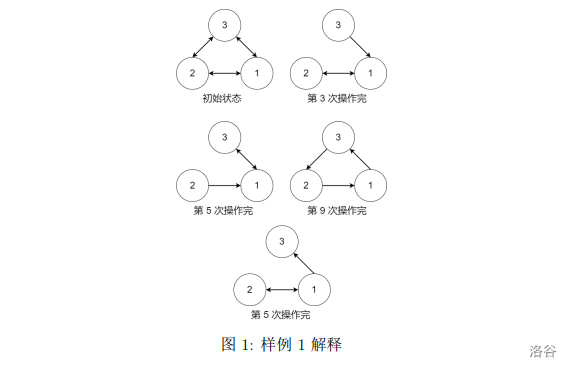
【样例 #2】
见附件中的galaxy/galaxy2.in与galaxy/galaxy2.ans。
【样例 #3】
见附件中的galaxy/galaxy3.in与galaxy/galaxy3.ans。
【样例 #4】
见附件中的galaxy/galaxy4.in与galaxy/galaxy4.ans。
【数据范围】
对于所有数据保证:1≤n≤5×1051 \le n \le 5 \times {10}^51≤n≤5×105,1≤m≤5×1051 \le m \le 5 \times {10}^51≤m≤5×105,1≤q≤5×1051 \le q \le 5 \times {10}^51≤q≤5×105。
本题需要使用文件输入输出,而非标准输入输出。
freopen("galaxy.in","r",stdin);
freopen("galaxy.out","w",stdout);
虫洞状态可以参考下面的图片, 图中的边表示存在且未被摧毁的虫洞:

【样例 #2】
见附件中的galaxy/galaxy2.in与galaxy/galaxy2.ans。
【样例 #3】
见附件中的galaxy/galaxy3.in与galaxy/galaxy3.ans。
【样例 #4】
见附件中的galaxy/galaxy4.in与galaxy/galaxy4.ans。
【数据范围】
对于所有数据保证:1≤n≤5×1051 \le n \le 5 \times {10}^51≤n≤5×105,1≤m≤5×1051 \le m \le 5 \times {10}^51≤m≤5×105,1≤q≤5×1051 \le q \le 5 \times {10}^51≤q≤5×105。
| 测试点 | n≤n \len≤ | m≤m \lem≤ | q≤q \leq≤ | 特殊限制 |
|---|---|---|---|---|
| 1∼31 \sim 31∼3 | 101010 | 202020 | 505050 | 无 |
| 4∼84 \sim 84∼8 | 103{10}^3103 | 104{10}^4104 | 103{10}^3103 | 无 |
| 9∼109 \sim 109∼10 | 5×1055 \times {10}^55×105 | 5×1055 \times {10}^55×105 | 5×1055 \times {10}^55×105 | 保证没有 t=2t = 2t=2 和 t=4t = 4t=4 的情况 |
| 11∼1211 \sim 1211∼12 | 5×1055 \times {10}^55×105 | 5×1055 \times {10}^55×105 | 5×1055 \times {10}^55×105 | 保证没有 t=4t = 4t=4 的情况 |
| 13∼1613 \sim 1613∼16 | 105{10}^5105 | 5×1055 \times {10}^55×105 | 5×1055 \times {10}^55×105 | 无 |
| 17∼2017 \sim 2017∼20 | 5×1055 \times {10}^55×105 | 5×1055\times 10^55×105 | 5×1055 \times {10}^55×105 | 无 |
本题需要使用文件输入输出,而非标准输入输出。
freopen("galaxy.in","r",stdin);
freopen("galaxy.out","w",stdout);