3513: 「一本通 6.6 练习 9」网格
内存限制:512 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:0
解决:0
题目描述
**原题来自:[BZOJ 3907](https://www.lydsy.com/JudgeOnline/problem.php?id=3907)**
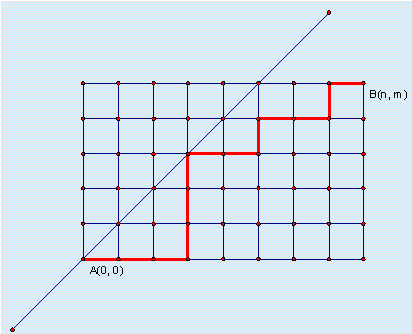
某城市的街道呈网格状,左下角坐标为 $A(0, 0)$,右上角坐标为 $B(n, m)$,其中 $n \ge m$。现在从 $A(0, 0)$ 点出发,只能沿着街道向正右方或者正上方行走,且不能经过图示中直线左上方的点,即任何途径的点 $(x, y)$ 都要满足 $x \ge y$,请问在这些前提下,到达 $B(n, m)$ 有多少种走法。
输入
仅有一行,包含两个整数 $n$ 和 $m$,表示城市街区的规模。
输出
仅有一个整数和一个换行/回车符,表示不同的方案总数。
样例输入 复制
6 6样例输出 复制
132提示
数据范围:对于全部数据,$1\le m\le n\le 5000$。