3449: 「一本通 5.4 练习 3」动物园

**原题来自：APIO 2007** 新建的圆形动物园是亚太地区的骄傲。圆形动物园坐落于太平洋的一个小岛上，包含一大圈围栏，每个围栏里有一种动物。如下图所示：  你是动物园的公关主管。你要做的是，让每个参观动物园的游客都尽可能高兴。今天有一群小朋友来到动物园参观，你希望能让他们在动物园度过一段美好的时光。但这并不是一件容易的事——有些小朋友喜欢某些动物，而有些小朋友则害怕某些动物。例如， Alex 喜欢可爱的猴子和考拉，而害怕拥有锋利牙齿的狮子。而 Polly 会因狮子有美丽的鬃毛而喜欢它，但害怕有臭味的考拉。 你可以选择将一些动物从围栏中移走以使得小朋友不会害怕。但你移走的动物也不能太多，否则留给小朋友们观赏的动物就所剩无几了。 每个小朋友站在大围栏圈的外面，可以看到连续的 $5$ 个围栏。你得到了所有小朋友喜欢和害怕的动物信息。当下面两处情况之一发生时，小朋友就会高兴： - 至少有一个他害怕的动物被移走； - 至少有一个他喜欢的动物没被移走。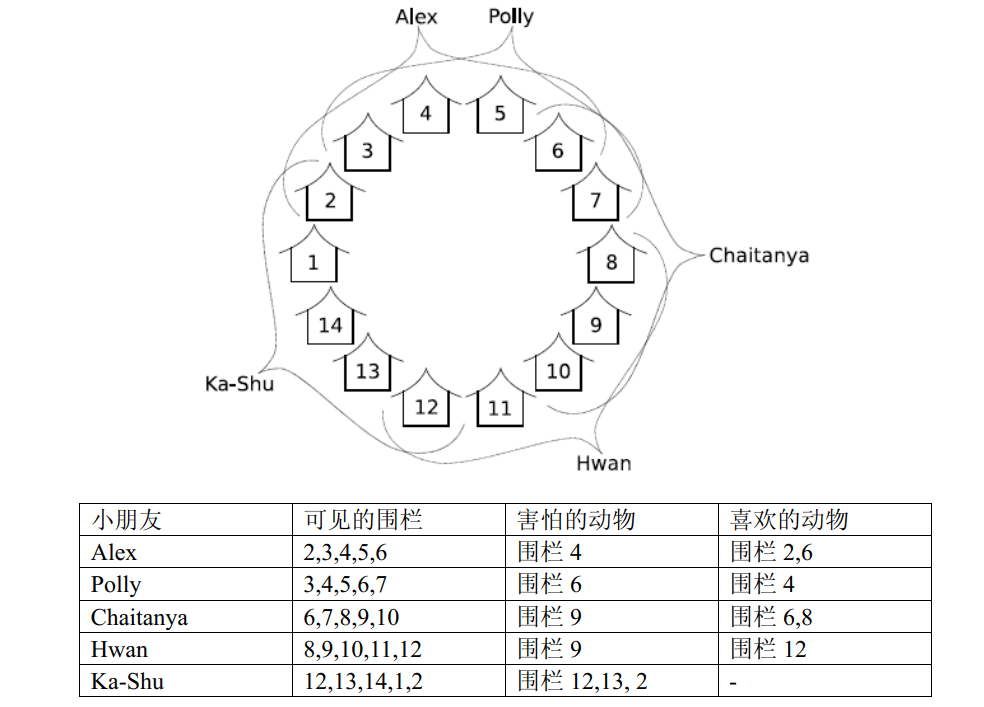 例如，考虑下图中的小朋友和动物：  假如你将围栏 $4$ 和 $12$ 的动物移走。Alex 和 Ka-Shu 将很高兴，因为至少有一个他们害怕的动物被移走了。这也会使 Chaitanya 高兴，因为他喜欢的围栏 $6$ 和 $8$ 中的动物都保留了。但是，Polly 和 Hwan 将不高兴，因为他们看不到任何他们喜欢的动物，而他们害怕的动物都还在。这种安排方式使得三个小朋友高兴。 现在换一种方法，如果你将围栏 $4$ 和 $6$ 中的动物移走，Alex 和 Polly 将很高兴，因为他们害怕的动物被移走了。Chaitanya 也会高兴，虽然他喜欢的动物 $6$ 被移走了，他仍可以看到围栏 $8$ 里面他喜欢的动物。同样的 Hwan 也会因可以看到自己喜欢的动物 $12$ 而高兴。唯一不高兴的只有 Ka-Shu。 如果你只移走围栏 $13$ 中的动物，Ka-Shu 将高兴，因为有一个他害怕的动物被移走了，Alex, Polly, Chaitanya 和 Hwan 也会高兴，因为他们都可以看到至少一个他们喜欢的动物。所以有 $5$ 个小朋友会高兴。这种方法使得了最多的小朋友高兴。

输入的第一行包含两个整数 $N, C$，用空格分隔。$N$ 是围栏数，$C$ 是小朋友的个数。围栏按照顺时针的方向编号为 $1,2,3,…,N$。 接下来的 $C$ 行，每行描述一个小朋友的信息，以下面的形式给出：$E \ F \ L \ X_1 \ X_2 \ \cdots X_F \ Y_1 \ Y_2\ \cdots Y_L$。 其中：$E$ 表示这个小朋友可以看到的第一个围栏的编号，换句话说，该小朋友可以看到的围栏为 $E, E+1, E+2, E+3, E+4$。注意，如果编号超过 $N$ 将继续从 $1$ 开始算。如：当 $N=14, E=13$ 时，这个小朋友可以看到的围栏为 $13,14,1, 2$ 和 $3$。 $F$ 表示该小朋友害怕的动物数。$L$ 表示该小朋友喜欢的动物数。 围栏 $X_1, X_2, \cdots , X_F$ 中包含该小朋友害怕的动物。围栏 $Y_1, Y_2,\cdots , Y_L$ 中包含该小朋友喜欢的动物。 $X_1, X_2, \cdots , X_F, Y_1, Y_2, \cdots , Y_L$ 是两两不同的整数，而且所表示的围栏都是该小朋友可以看到的。 小朋友已经按照他们可以看到的第一个围栏的编号从小到大的顺序排好了（这样最小的 $E$ 对应的小朋友排在第一个，最大的 $E$ 对应的小朋友排在最后一个）。 注意可能有多于一个小朋友对应的 $E$ 是相同的。

仅输出一个数，表示最多可以让多少个小朋友高兴。

14 5
2 1 2 4 2 6
3 1 1 6 4
6 1 2 9 6 8
8 1 1 9 12
12 3 0 12 13 2

5