1966: 【基础】人造星空-标记法
内存限制:128 MB
时间限制:1.000 S
评测方式:文本比较
命题人:
提交:35
解决:26
题目描述
A市利用无人机制造了一个n*m大小的人造星空,在这个n*m大小的星空中,每个点都有一个无人机,无人机有发光和不发光两种不同的状态,对于所有的发光点,在空中就能形成独特的星空图形。
图形中有多个不同的图案,同一个图案的定义是这样的,对于两个发光的点,如果他们的曼哈顿距离(对于A(x1,y1)和B(x2,y2),A和B之间的曼哈顿距离为|x1-x2|+|y1-y2|)小于等于2,那么这两个点就属于一个图案。
请你编程计算一下,这个n*m的图形中,有多少个不同的图案。
比如:一个6 * 6的图形如下,该图形中有2个符合条件的图案。
-#----
##----
--##--
------
-#----
--#-##
图形中有多个不同的图案,同一个图案的定义是这样的,对于两个发光的点,如果他们的曼哈顿距离(对于A(x1,y1)和B(x2,y2),A和B之间的曼哈顿距离为|x1-x2|+|y1-y2|)小于等于2,那么这两个点就属于一个图案。
请你编程计算一下,这个n*m的图形中,有多少个不同的图案。
比如:一个6 * 6的图形如下,该图形中有2个符合条件的图案。
-#----
##----
--##--
------
-#----
--#-##
输入
第一行,两个数n和m。(1<=n,m<=100)
接下来一共n行,每行m个字符。对于第i行第j个字符,如果其为“-”,那么表示该点不发光,如果其为“#”,那么表示该点发光。不可能出现其他的字符。
接下来一共n行,每行m个字符。对于第i行第j个字符,如果其为“-”,那么表示该点不发光,如果其为“#”,那么表示该点发光。不可能出现其他的字符。
输出
输出一个整数,代表图案的个数。
样例输入 复制
6 6
-#----
##----
--##--
------
-#----
--#-##样例输出 复制
2提示
符合题意的点的示意图如下:(当前点的周围12个点)
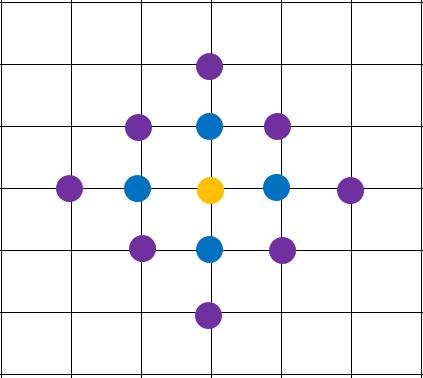
即:搜索连通图的数量


即:搜索连通图的数量
